以有尽对无尽——等量代换的应用

上次参加比赛时，看到一个有趣的题目。

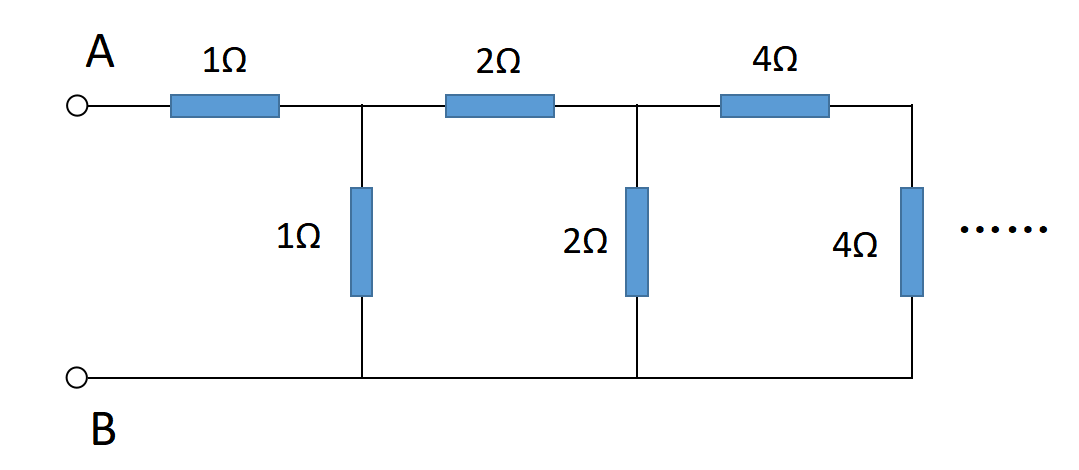
如图有一个无限延伸的电阻网，求AB间的等效电阻。

如果电阻网是有限的，我们可以通过公式

$$R_并=\frac{R_1R_2}{R_1+R_2}$$

$$R_串=R_1+R_2$$

直接算出电阻值。

但在无穷面前，这种方法就显得苍白无力。

在解这道题时，我联想到某乎上的一个数学问题：如何证明0.999…=1？

一个方法是，设P=0.999…①，

则P/10=0.099…②。

注意到0.999…-0.099…=0.9，

∴①-②得9P/10=0.9。

∴P=1，即0.999…=1。

这种替换（好吧应该是消去）无穷的方法，就叫等量代换。

回到这个题，观察$R_{AB}$，发现它可以拆分成两部分：

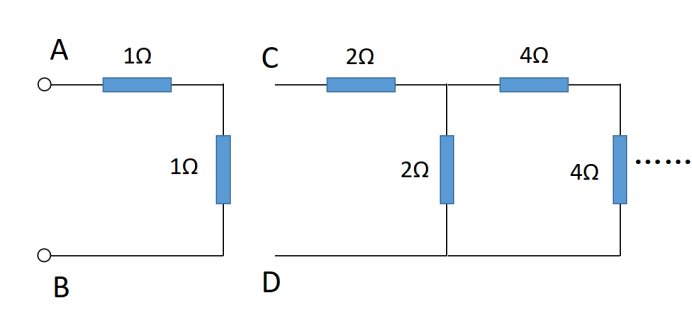
不难发现，

$$R_{CD}=2R_{AB}$$

再由串并联公式可得：

$$R_{AB}=1+\frac{R_{CD}}{1+R_{CD}}=\frac{4R_{AB}+1}{2R_{AB}+1}$$

解得：

$$R_{AB}=\frac{1+\sqrt{3}}{2}$$

另外，在解无限连分数中也有此方法的应用：

$$\sqrt{2}=1+\frac{1}{2+\frac{1}{2+\frac{1}{2+\ddots}}}$$

而关于如何构造连分数即它的其他性质，又是另一回事了（剧透）。

下期十年后随缘更新

Ciallo～ (∠・ω< )⌒☆